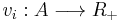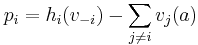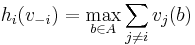Vickrey–Clarke–Groves auction
A Vickrey–Clarke–Groves (VCG) auction of multiple goods is a sealed-bid auction wherein bidders report their valuations for the items. The auction system assigns the items in a socially optimal manner, while ensuring each bidder receives at most one item. This system charges each individual the harm they cause to other bidders,[1] and ensures that the optimal strategy for a bidder is to bid the true valuations of the objects. It is a generalization of a Vickrey auction for multiple items.
The auction is named after William Vickrey, Edward H. Clarke, and Theodore Groves.
Contents |
A Formal Description
For any set of auctioned items  and a set of bidders
and a set of bidders 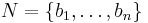 , let
, let 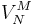 the social value of the VCG auction for a given bid-combination. A bidder
the social value of the VCG auction for a given bid-combination. A bidder 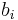 who wins an item
who wins an item 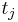 pays
pays 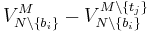 , which is the social cost of his winning that is incurred by the rest of the agents
, which is the social cost of his winning that is incurred by the rest of the agents
Indeed, the set of bidders other than 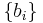 is
is 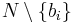 . When item
. When item 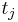 is available, they could attain welfare
is available, they could attain welfare 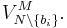 The winning of the item by
The winning of the item by 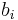 reduces the set of available items to
reduces the set of available items to 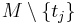 , however, so that the attainable welfare is now
, however, so that the attainable welfare is now 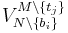 . The difference between the two levels of welfare is the payment for
. The difference between the two levels of welfare is the payment for 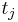 paid by the winning bidder
paid by the winning bidder 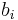 .
.
The winning bidder who has value  for the item
for the item 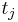 derives therefore utility
derives therefore utility 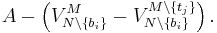
Examples
Example #1
See the example with apples in the introduction of Vickrey Auction.
Example #2
Assume that there are two bidders, 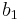 and
and 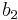 , two items,
, two items, 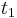 and
and 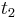 , and each bidder is allowed to obtain one item. We let
, and each bidder is allowed to obtain one item. We let 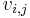 be bidder
be bidder 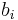 's valuation for item
's valuation for item 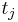 . Assume
. Assume 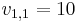 ,
, 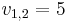 ,
, 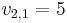 , and
, and 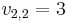 . We see that both
. We see that both 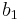 and
and 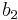 would prefer to receive item
would prefer to receive item 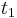 ; however, the socially optimal assignment gives item
; however, the socially optimal assignment gives item 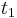 to bidder
to bidder 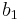 (so his achieved value is
(so his achieved value is 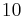 ) and item
) and item 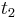 to bidder
to bidder 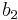 (so his achieved value is
(so his achieved value is 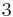 ). Hence, the total achieved value is
). Hence, the total achieved value is 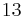 , which is optimal.
, which is optimal.
If person 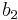 were not in the auction, person
were not in the auction, person 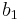 would still be assigned to
would still be assigned to 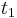 , and hence no harm was done for that bidder. Hence,
, and hence no harm was done for that bidder. Hence, 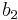 is charged nothing.
is charged nothing.
If person 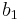 were not in the auction, person
were not in the auction, person 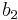 would be assigned to
would be assigned to 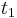 , and would have valuation
, and would have valuation 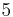 .
. 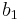 thus caused
thus caused 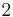 harm to
harm to 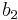 , and hence
, and hence 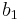 is charged
is charged 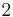 .
.
Optimality of Truthful Bidding
The following is a proof that bidding one's true valuations for the auctioned items is optimal[2]
For each bidder 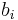 , let
, let 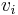 be her true valuation of an item
be her true valuation of an item 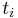 , and suppose (without loss of generality) that
, and suppose (without loss of generality) that 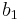 wins
wins 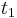 upon submitting his true valuations.
upon submitting his true valuations.
Note that the size bid of 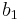 has no effect on her utility as long as she wins the item (see the utility function above). Hence, we assume that
has no effect on her utility as long as she wins the item (see the utility function above). Hence, we assume that 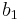 does not bid truthfully, and receives item
does not bid truthfully, and receives item 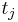 because of his non-truthful bidding. In the truthful bidding case,
because of his non-truthful bidding. In the truthful bidding case, 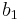 has total utility
has total utility 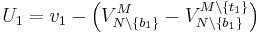 . In the untruthful bidding case,
. In the untruthful bidding case, 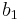 has total utility
has total utility 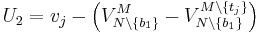 . Hence, we must prove that
. Hence, we must prove that 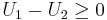 , which shows that the utility received from truthful bidding is always at least that received from untruthful bidding.
, which shows that the utility received from truthful bidding is always at least that received from untruthful bidding.
However, the first term there is the maximum total social value achieved when 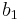 received
received 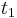 , and the second term there is the maximum total social value achieved when
, and the second term there is the maximum total social value achieved when 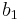 received
received 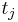 . However, we assumed that the VCG auction gave
. However, we assumed that the VCG auction gave 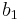 item
item 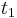 ; hence, the first term must be greater, and
; hence, the first term must be greater, and 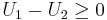 .
.
More general setting
We can consider a more general setting[3] of the VCG mechanism. Consider a set  of possible outcomes and
of possible outcomes and  bidders which have different valuations for each outcome. This can be expressed as, function
bidders which have different valuations for each outcome. This can be expressed as, function
for each bidder  which expresses the value it has for each alternative. In this auction, each bidder will submit his valuation and the VCG mechanism will choose the alternative
which expresses the value it has for each alternative. In this auction, each bidder will submit his valuation and the VCG mechanism will choose the alternative 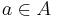 that maximizes
that maximizes 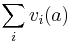 and charge prices
and charge prices 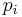 given by:
given by:
where 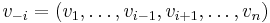 , that is,
, that is, 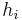 is a function that only depends on the valuation of the other players. This alone gives a truthful mechanism, that is, a mechanism where bidding the true valuation is a dominant strategy.
is a function that only depends on the valuation of the other players. This alone gives a truthful mechanism, that is, a mechanism where bidding the true valuation is a dominant strategy.
We could take, for example, 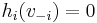 , but we would have all prices negative, what might not be desirable - we would rather prefer that players give money to the mechanism than the other way round. The function:
, but we would have all prices negative, what might not be desirable - we would rather prefer that players give money to the mechanism than the other way round. The function:
is called Clarke pivot rule. It has some very good properties as:
- it is individually rational, i.e.,
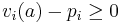 . It means that all the players are getting positive utility by participating in the auction. No one is really being forced do bid.
. It means that all the players are getting positive utility by participating in the auction. No one is really being forced do bid.
- it has no positive transfers, i.e.,
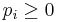 . So the mechanism doesn't need to pay anything to the bidders.
. So the mechanism doesn't need to pay anything to the bidders.
References
- ^ von Ahn, Luis (2008-10-07). "Sponsored Search" (PDF). 15–396: Science of the Web Course Notes. Carnegie Mellon University. http://scienceoftheweb.org/15-396/lectures/lecture11.pdf. Retrieved 2008-11-05.
- ^ von Ahn, Luis (2008-10-07). "Assignment 5 Solutions" (PDF). 15–396: Science of the Web Published Solutions. Carnegie Mellon University. http://www.scienceoftheweb.org/15-396/assignments/assignment5_solutions.pdf. Retrieved 2008-11-05.
- ^ Nisan, Roughgarden, Tardos and Vazirani, Algorithmic Game Theory, Cambridge, 2007
![U_1 - U_2 = v_1 - \left(V^{M}_{N \setminus \{b_1\}} - V^{M \setminus \{t_1\}}_{N \setminus \{b_1\}}\right) - v_j %2B \left(V^{M}_{N \setminus \{b_1\}}-V^{M \setminus \{t_j\}}_{N \setminus \{b_1\}}\right) = \left[v_1 %2B V^{M \setminus \{t_1\}}_{N \setminus \{b_1\}}\right] - \left[v_j %2B V^{M \setminus \{t_j\}}_{N \setminus \{b_1\}}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/f75caf7a814b080c6029de7ef204134b.png)